Matematica e natura: la successione di Fibonacci
La successione di Fibonacci è una successione di numeri naturali che riveste un’importanza fondamentale per le sue proprietà matematiche e per i suoi risvolti ed utilizzi sia in natura che nella vita di tutti i giorni.
I primi due membri della successione sono i numeri 0 ed 1; tutti i termini successivi si trovano sommando i due termini precedenti. Pertanto i primi termini della successione saranno:
0
1
0+1=1
1+1=2
2+1=3
3+2=5
5+3=8
e così via a formare la successione:
1
0+1=1
1+1=2
2+1=3
3+2=5
5+3=8
e così via a formare la successione:
0,1,1,2,3,5,8,13,21,34, 55, 89…
Fibonacci e i conigli. Leonardo Fibonacci, conosciuto come Leonardo Pisano, nacque a Pisa all’incirca verso il 1170 dc. Per le sue scoperte in ambito matematico è stato definito come il più grande matematico europeo del medioevo. Data la volontà del padre di farlo diventare mercante, fu istruito nelle teniche di calcolo, specialmente quelle indo-arabiche, ancora sconosciute in Italia. Il fatto che il padre era responsabile del commercio pisano in Algeria fece si che il giovane Leonardo viaggiasse dapprima in Algeria e poi in Siria, Egitto e Grecia, dato che nel frattempo aveva ereditato il lavoro del padre. Verso il 1200 tornò in Italia, dove si dedicò ai suoi studi matematici. La sua opera più importante fu il Liber Abaci, dove descrisse il sistema di numerazione indiana ed introdusse l’uso dello 0. La successione che porta il suo nome venne introdotta per risolvere un problema legato alla natalità dei conigli.
Supponendo di partire da una coppia di conigli, Fibonacci voleva trovare una legge che descrivesse la crescita di una popolazione di conigli assumendo che:
Supponendo di partire da una coppia di conigli, Fibonacci voleva trovare una legge che descrivesse la crescita di una popolazione di conigli assumendo che:
- la prima coppia diventi fertile al compimento del primo mese e dia alla luce una nuova coppia al compimento del secondo mese;
- le nuove coppie nate si comportino in modo analogo
Ne risulta la successione 0,1,2,3,5,8,13,21,34,55,89… detta Successione di Fibonacci.
La successione di Fibonacci ed il rapporto aureo. La successione di Fibonacci possiede delle caratteristiche sorprendenti e di grande interesse. La principale è senza dubbio quella per cui il rapporto tra due membri consecutivi della serie tende al rapporto aureo (o numero di Fidia)
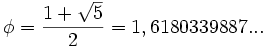
Infatti, :
1/1 = 1, 2/1 = 2, 3/2 = 1·5, 5/3 = 1·666…, 8/5 = 1·6, 13/8 = 1·625, 21/13 = 1·61538…
mano a mano che si va avanti questo rapporto si avvicina sempre più al valore del rapporto aureo; il perchè di questo fatto non è assolutamente noto. Questo rapporto è quello che esiste tra due segmenti a e b per i quali il rapporto tra a e b sia uguale a quello tra la somma (a+b) ed a. Sia le sue proprietà geometriche e matematiche, che la frequente riproposizione in svariati contesti naturali e culturali, apparentemente non collegati tra loro, hanno impressionato nei secoli la mente dell’uomo, che è arrivato a cogliervi col tempo un ideale di bellezza e armonia, spingendosi a ricercarlo e, in alcuni casi, a ricrearlo nell’ambiente antropico quale “canone di bellezza”; testimonianza ne è forse la storia del nome che in epoche più recenti ha assunto gli appellativi di “aureo” o “divino”, proprio a dimostrazione del fascino esercitato. Molte opere pittoriche o architettoniche sono state costruite con proporzioni esattamente uguali al rapporto aureo; queste proporzioni sono, per esempio, alla base delle piramidi egizie, come del tempio greco, del duomo romano e delle cattedrali gotiche.
Alcune caratteristiche della successione di Fibonacci.
Quadrati
Se si prendono due numeri di Fibonacci consecutivi e se ne fa il quadrato, la somma fra i quadrati è un altro numero di Fibonacci che nella sequenza occupa il posto risultante dalla somma delle posizioni dei due termini di partenza. Esempio:
Quadrati
Se si prendono due numeri di Fibonacci consecutivi e se ne fa il quadrato, la somma fra i quadrati è un altro numero di Fibonacci che nella sequenza occupa il posto risultante dalla somma delle posizioni dei due termini di partenza. Esempio:
32+52=34
e infatti 3 è il 4° numero di Fibonacci, 5 è il 5° numero di Fibonacci e 34 è il 9° numero di Fibonacci oppure
82+132= 233
e 233 è il 13° numero di Fibonacci.
Ultime cifre
Analizzando la successione
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…
ed evidenziando le ultime cifre si ha la seguente successione:
0, 1, 1, 2, 3, 5, 8, 3, 1, 4, 5, 9, 4, 3, 7, 0, 7, …
Bene, questa successione si ripete uguale dopo i primi 60 termini, cioè ha un ciclo pari a 60, e così via per tutta l’infinita successione di Fibonacci. M la cosa sorprendente è che tali regolarità compaiono anche se si prendono in esame più di una cifra finale: infatti due cifre finali hanno un ciclo pari a 300 (cioè dopo i primi 300 numeri si ripetono per altri 300 e così via…), tre cifre hanno un ciclo pari a 1500, quattro cifre pari a 15000, cinque cifre pari a 150000 e cosi via…
Altre proprietà
- Il quadrato di un termine di FIbonacci può essere espresso come il prodotto del numero precedente e del del numero successivo, aumentato o diminuito di 1. Per esempio moltiplicando 3 ed 8 (rispettivamente 4° e 6° numero di Fibonacci), otteniamo 24, che è dato dal quadrato di 5 (5° numero di Fibonacci) a cui è stato sottratto 1.
- Ogni numero di Fibonacci corrisponde alla somma dei numeri che lo precedono eccetto l’ultimo, aumentata di 1.
- Se si prende la sequenza dei quadrati dei numeri di Fibonacci, e si costruisce una sequenza sommando a due a due i numeri della prima sequenza, la sequenza risultante è costituita da tutti e soli i numeri di Fibonacci di posto dispari.
- Data la sequenza dei numeri di Fibonacci di posto dispari, se si costruisce la sequenza ottenuta sottraendo a due a due i numeri adiacenti della prima sequenza, si ottiene la sequenza dei numeri di Fibonacci di posto pari.
 La successione di Fibonacci in natura. La spirale logaritmica è una curva costruita a partire dai numeri di Fibonacci: se si costruiscono infatti due quadranti contigui di lato 1 e poi aggiungiamo un quadrato di lato 2, seguito da un’altro di lato 3, poi di lato 5 … e congiungiamo con una curva i vertici di questi quadrati, otteniamo una spirale, detta spirale logaritmica, che in natura è presente nella forma delle conchiglie, nella disposizione dei semi nel girasole, nelle pigne o nei cavolfiori.
La successione di Fibonacci in natura. La spirale logaritmica è una curva costruita a partire dai numeri di Fibonacci: se si costruiscono infatti due quadranti contigui di lato 1 e poi aggiungiamo un quadrato di lato 2, seguito da un’altro di lato 3, poi di lato 5 … e congiungiamo con una curva i vertici di questi quadrati, otteniamo una spirale, detta spirale logaritmica, che in natura è presente nella forma delle conchiglie, nella disposizione dei semi nel girasole, nelle pigne o nei cavolfiori. In molte specie vegetali, prime fra tutte le Astaracee (girasoli, margherite, ecc.), il numero dei petali di ogni fiore è di solito un numero di Fibonacci, come 5, 13, 55 o perfino 377, come nel caso della diaccola. Le brattee delle pigne si dispongono in due serie di spirali dal ramo verso l’esterno – una in senso orario e l’altra in senso antiorario. Le scaglie degli ananas presentano un’aderenza ancora più costante ai fenomeni di Fibonacci: non una sola eccezione fu trovata in un test compiuto su 2000 ananas.
In molte specie vegetali, prime fra tutte le Astaracee (girasoli, margherite, ecc.), il numero dei petali di ogni fiore è di solito un numero di Fibonacci, come 5, 13, 55 o perfino 377, come nel caso della diaccola. Le brattee delle pigne si dispongono in due serie di spirali dal ramo verso l’esterno – una in senso orario e l’altra in senso antiorario. Le scaglie degli ananas presentano un’aderenza ancora più costante ai fenomeni di Fibonacci: non una sola eccezione fu trovata in un test compiuto su 2000 ananas.I numeri di Fibonacci si trovano anche nella fillotassi, l’ordinamento delle foglie su un gambo. Fu Keplero a rilevare che su molti tipi di alberi le foglie sono allineate secondo uno schema che comprende due numeri di Fibonacci. Partendo da una foglia qualunque, dopo uno, due, tre o cinque giri dalla spirale si trova sempre una foglia allineata con la prima e a seconda delle specie, questa sarà la seconda, la terza, la quinta, l’ottava o la tredicesima foglia.
Questa successione si ritrova anche nel corpo umano: il rapporto fra le falangi di un dito di un uomo adulto, infatti, formano una piccola serie di Fibonacci.
Infine, i numeri di Fibonacci hanno utilizzi anche nel campo dell’economia, con la teoria ad onde di Elliot, per prevedere l’andamento dei titoli di borsa e nell’informatica; in particolare, vi è un complesso meccanismo basato su tali numeri, detto “Fibonacci heap” che viene utilizzato nel processore Pentium della Intel per la risoluzione di particolari algoritmi.
2,611 total views, 4 views today





