La magia dei numeri primi
I numeri primi sono dei numeri molto importanti nel mondo matematico; si definisce primo un numero che è divisibile solo per 1 e per se stesso. Sono numeri primi 2,3,5,7,11,13…I primi studi sui numeri primi si possono attribuire a Euclide, tra il IV ed il III secolo a.c., ma il grosso impulso è stato dato da Gauss, Fermat, e sopratutto da Bernard Riemann nel corso del XIX° secolo.
I mattoni della matematica. I numeri primi sono i mattoni costituenti di ogni numero naturale; il teorema fondamentale dell’aritmetica afferma infatti che ogni numero naturale può essere ottenuto dalla moltiplicazione di numeri primi, e l’nsieme di questi numeri primi è unico. Prendiamo per esempio il numero 140: questo può essere ottenuto dalla moltiplicazione di 2*2*5*7, tutti numeri primi. Non ci sono altri gruppi di numeri primi che moltiplicati tra loro danno come risultato il numero 140. Un’altra caratteristica dei numeri primi è che ne esistono infiniti: sebbene il loro numero tende a diminuire mano a mano che si va avanti nella ricerca, Euclide scoprì che ne esiste comunque una infinità.
A caccia di regolarità. La successione dei numeri primi è apparentemente irregolare e non esiste ad oggi una formula che consenta di ricavare tutti i numeri primi. I matematici, soprattutto Gauss, sono però riusciti a trovare delle regolarità molto importanti. Analizzando infatti la tabella, che riporta nella seconda colonna il numero di primi compresi in quell’intervallo e nella terza colonna la frazione tra il numero dei primi ed il totale dei numeri considerati questa regolarità viene fuori in tutta la sua chiarezza. Moltiplicando per 10 l’insieme dei numeri, il valore della terza colonna aumenta sempre di circa 2,3, una relazione di chiaro stampo logaritmico. 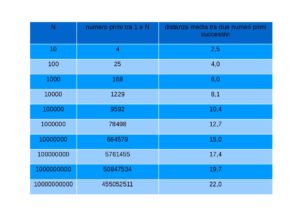
Numeri primi in natura. La principale caratteristica dei numeri primi, cioè quella di non avere divisori oltre a 1 e a se stessi, ha delle importanti applicazioni anche in ambito naturale: esistono infatti due specie di cicale, la Magicicada septendecim e la Magicicada tredecim, che hanno un ciclo di vita rispettivamente di 17 e 13 anni. Queste cicale vivono sotto terra nello stato di ninfe per tutti gli anni tranne l’ultimo, quando passano allo stato adulto ed escono dal terreno per alimentarsi, accoppiarsi e deporre le uova. Il fatto che i lori cicli siano numeri primi, garantisce che le due specie dovranno dividere l’ambiente solo una volta ogni 201 anni (17 x 13) ed evitando quindi alle due specie di cicale una competizione eccessiva.
Numeri primi e carte di credito. I numeri primi compaiono nella nostra vita di tutti i giorni molto più spesso di quanto noi ce ne possiamo rendere conto: quando facciamo un acquisto e paghiamo con la carta di credito, la nostra transazione è messa in sicurezza proprio grazie all’utilizzo di numeri primi. In particolare, l’azienda ci invia due numeri molto grandi, uno dei quali è dato dalla moltiplicazione di due numeri primi essi stessi di molte cifre (circa 60), con cui “occultare” il nostro numero di carta di credito. Grazie poi ad un altro numero conosciuto solo dall’azienda, e grazie ad un teorema (il piccolo teorema di Fermat) che spiega alcune proprietà dei numeri primi, l’azienda stessa può risalire al numero originale della carta. La sicurezza di questo metodo sta tutta nel fatto che la fattorizzazione in numeri primi è molto complicata, per numeri così grandi, quindi è altamente improbabile che un hacker possa risalire ai due numeri primi utilizzati dall’azienda.
Problemi aperti. I numeri primi sono una fucina di congetture ancora da dimostrare. La più importante è forse l‘Ipotesi di Riemann, la quale, se dimostrata, implicherebbe una sorta di regolarità nella distribuzione dei numeri primi. La congettura di Goldbach afferma invece che ogni numero pari maggiore di due può essere scritto come somma di due numeri primi: anche in questo caso si è in attesa di una dimostrazione matematica. Infine: quante coppie di numeri primi gemelli esistono (cioè numeri primi distanti solo due unità, come 11 e 13)? Euclide affermò che ne esistono infinite, ma nessuno è ancora riuscito a dimostrarlo.
2,127 total views, 17 views today




